题目描述
九条可怜是一个喜欢计算几何的女孩子,她画了一个特别的平面坐标系,其中 $x$ 轴正半轴与 $y$ 轴正半轴夹角为 $60$ 度。
从中,她取出所有横纵坐标不全为偶数,且满足 $-2 a + 1 \le x \le 2 a - 1$,$-2 b + 1 \le y \le 2 b - 1$,$-2 c + 1 \le x + y \le 2 c - 1$ 的整点。
可怜想将其中一些点染色,但相邻的点不能同时染色。具体地,对于点 $(x, y)$,它和 $(x, y + 1), (x, y - 1), (x + 1, y), (x - 1, y), (x + 1, y - 1), (x - 1, y + 1)$ 六个点相邻,可结合样例解释理解。
可怜想知道在这个规则下最多能将多少点染色,以及染最多点的染色方案数。由于后者值可能很大,对于染色方案数,你只需要输出对 $998244353$ 取模后的结果。注意不需要将最多染色点数取模。
输入格式
第一行一个整数 $T$ 代表数据组数。
接下来 $T$ 行,每行三个整数 $a, b, c$ 代表一组数据。
输出格式
输出共 $T$ 行,每行两个整数,代表最多能染的点数(不取模)和方案数对 $998244353$ 取模的结果。
样例一
input
6 2 1 2 1 1 137 3 94 95 3 1998 1996 998244 353999 999999 50 120 150
output
7 4 4 1 1124 31585548 23951 33873190 1289433675488 748596399 23600 480090154
explanation
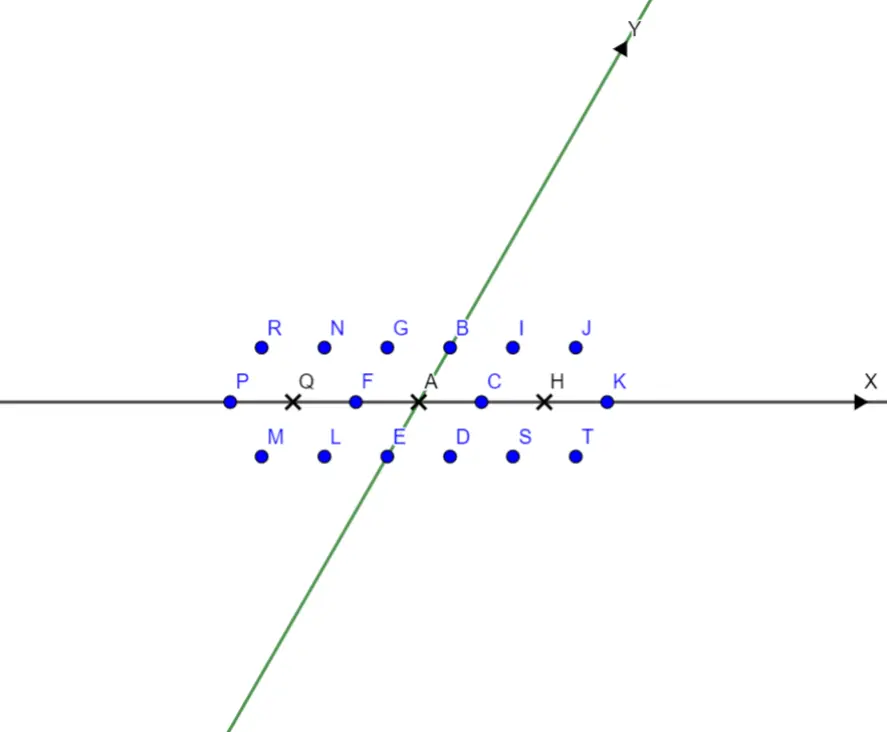
如下图所示,点 $J$ 的坐标为 $(2, 1)$,点 $F$ 的坐标为 $(-1, 0)$,点 $H$ 的坐标为 $(2, 0)$。在这三个点中,只有点 $H$ 是横纵坐标全为偶数的点。图中与点 $A$ 距离为 $1$ 的点有 $B C D E F G$ 六个点。
在样例的第一组数据中,满足条件的整点有 $N G B I J P F C K M L E D S T$。
最多能染 $7$ 个点,方案共 $4$ 种,具体为:$P N L B D J T$,$R M F B D J T$,$R M G E C J T$,$R M G E I S K$。
在样例的第二组数据中,满足条件的整点有 $G B I F C L E D$。
最多能染 $4$ 个点,方案共 $1$ 种,具体为:$L G I D$。
限制与约定
对于所有测试点:$1 \le T \le 10$,$1 \le a, b, c \le {10}^6$。
每个测试点的具体限制见下表:
| 测试点编号 | $a \le$ | $b, c \le$ | 特殊限制 |
|---|---|---|---|
| $1$ | $3$ | $3$ | $a = b = c$ |
| $2$ | $4$ | $4$ | $a = b = c$ |
| $3$ | $4$ | $4$ | 无 |
| $4$ | $3$ | $100$ | 无 |
| $5 \sim 6$ | $3$ | $1000$ | 无 |
| $7 \sim 8$ | $3$ | $5000$ | 无 |
| $9 \sim 10$ | $100$ | $100$ | $a = b = c$ |
| $11 \sim 14$ | $100$ | $100$ | 无 |
| $15$ | ${10}^5$ | ${10}^5$ | $a = b = c$ |
| $16$ | ${10}^5$ | ${10}^5$ | 无 |
| $17 \sim 18$ | ${10}^6$ | ${10}^6$ | $a \cdot b \cdot c \le {10}^6$ |
| $19$ | ${10}^6$ | ${10}^6$ | $a = b = c$ |
| $20$ | ${10}^6$ | ${10}^6$ | 无 |
